Der Code für diesen Blog ist zusammen mit dem Datensatz unter dem folgenden Link verfügbar https://github.com/shekharpandey89/k-means
K-Means-Clustering ist ein unbeaufsichtigter maschineller Lernalgorithmus. Wenn wir den K-Means-Algorithmus für unüberwachtes Clustering mit dem überwachten Algorithmus vergleichen, ist es nicht erforderlich, das Modell mit den markierten Daten zu trainieren. Der K-Means-Algorithmus wird verwendet, um verschiedene Objekte basierend auf ihren Attributen oder Merkmalen in eine Anzahl von K Gruppen zu klassifizieren oder zu gruppieren. Hier ist K eine ganze Zahl. Das K-Means berechnet den Abstand (unter Verwendung der Abstandsformel) und findet dann den minimalen Abstand zwischen den Datenpunkten und dem Schwerpunktcluster, um die Daten zu klassifizieren.
Lassen Sie uns die K-Means anhand des kleinen Beispiels mit den 4 Objekten verstehen, und jedes Objekt hat 2 Attribute.
| Objektname | Attribut_X | Attribut_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-Mittel, um numerisches Beispiel zu lösen:
Um das obige numerische Problem durch K-Means zu lösen, müssen wir die folgenden Schritte ausführen:
Der K-Means-Algorithmus ist sehr einfach. Zuerst müssen wir eine beliebige Anzahl von K wählen und dann die Schwerpunkte oder das Zentrum der Cluster auswählen. Um die Schwerpunkte zu wählen, können wir eine beliebige Anzahl von Objekten für die Initialisierung auswählen (abhängig vom Wert von K).
Die grundlegenden Schritte des K-Means-Algorithmus sind wie folgt:
- Läuft weiter, bis sich keine Objekte aus ihren Schwerpunkten bewegen (stabil).
- Wir wählen zunächst zufällig einige Schwerpunkte aus.
- Dann bestimmen wir den Abstand zwischen jedem Objekt und den Schwerpunkten.
- Gruppieren der Objekte nach Mindestabstand.
Jedes Objekt hat also zwei Punkte als X und Y, und sie stellen sich auf dem Graphenraum wie folgt dar:
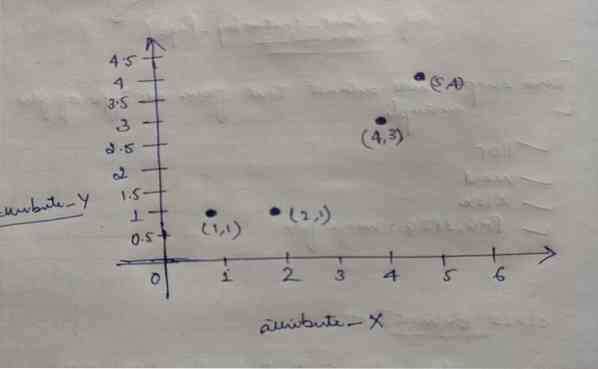
Wir wählen also zunächst den Wert von K=2 als zufällig, um unser obiges Problem zu lösen.
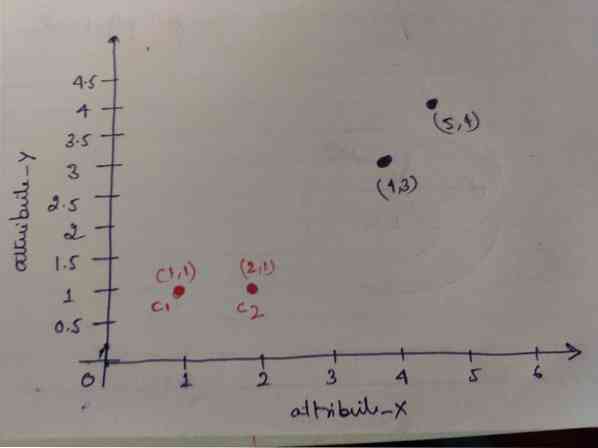
Schritt 1: Zunächst wählen wir die ersten beiden Objekte (1, 1) und (2, 1) als unsere Schwerpunkte. Die folgende Grafik zeigt dasselbe. Wir nennen diese Schwerpunkte C1 (1, 1) und C2 (2,1). Hier können wir sagen C1 ist Gruppe_1 und C2 ist Gruppe_2.
Schritt 2: Jetzt berechnen wir jeden Objektdatenpunkt zu Schwerpunkten unter Verwendung der euklidischen Distanzformel.
Um die Entfernung zu berechnen, verwenden wir die folgende Formel.

Wir berechnen den Abstand von Objekten zu Schwerpunkten, wie im Bild unten gezeigt.

Also haben wir die Entfernung jedes Objektdatenpunkts durch die obige Entfernungsmethode berechnet und schließlich die Entfernungsmatrix wie unten angegeben erhalten:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) Cluster1 | Gruppe 1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) Cluster2 | Gruppe_2 |
| EIN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Ja |
Jetzt haben wir den Abstandswert jedes Objekts für jeden Schwerpunkt berechnet. Zum Beispiel haben die Objektpunkte (1,1) einen Abstandswert zu c1 ist 0 und c2 ist 1.
Da wir aus der obigen Distanzmatrix herausfinden, dass das Objekt (1, 1) einen Abstand zu Cluster1 (c1) hat 0 und zu Cluster2 (c2) ist 1. Das Objekt eins ist also nahe bei Cluster1 selbst.
Wenn wir das Objekt (4, 3) überprüfen, beträgt der Abstand zu Cluster1 3.61 und zu Cluster2 ist 2.83. Das Objekt (4, 3) verschiebt sich also zu Cluster2.
Wenn Sie nach dem Objekt (2, 1) suchen, beträgt der Abstand zu Cluster1 1 und zu Cluster2 0. Also verschiebt sich dieses Objekt zu Cluster2.
Nun gruppieren wir die Punkte nach ihrem Entfernungswert (Objekt-Clustering).
G_0 =
| EIN | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | Gruppe 1 |
| 0 | 1 | 1 | 1 | Gruppe_2 |
Nun gruppieren wir die Punkte nach ihrem Entfernungswert (Objekt-Clustering).
Und schließlich sieht das Diagramm nach dem Clustering (G_0) wie unten aus.
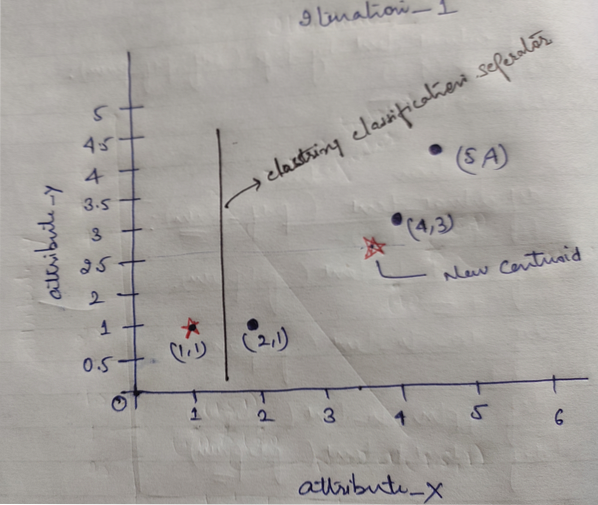
Iteration_1: Jetzt berechnen wir neue Schwerpunkte, wenn sich die Anfangsgruppen aufgrund der Abstandsformel geändert haben, wie in G_0 . gezeigt. Die Gruppe_1 hat also nur ein Objekt, ihr Wert ist also immer noch c1 (1,1), aber die Gruppe_2 hat 3 Objekte, also ist ihr neuer Schwerpunktwert 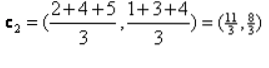
Also, neue c1 (1,1) und c2 (3.66, 2.66)
Jetzt müssen wir wieder den gesamten Abstand zu neuen Schwerpunkten berechnen, wie wir zuvor berechnet haben.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) Cluster1 | Gruppe 1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) Cluster2 | Gruppe_2 |
| EIN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Ja |
Iteration_1 (Objekt-Clustering): Nun, im Auftrag der neuen Distanzmatrix (DM_1)-Berechnung, gruppieren wir sie entsprechend. Also verschieben wir das M2-Objekt von group_2 zu group_1 als Regel für den Mindestabstand zu den Schwerpunkten, und der Rest des Objekts ist gleich. Das neue Clustering wird also wie folgt sein.
G_1 =
| EIN | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | Gruppe 1 |
| 0 | 0 | 1 | 1 | Gruppe_2 |
Jetzt müssen wir die neuen Schwerpunkte erneut berechnen, da beide Objekte zwei Werte haben.
Es werden also neue Schwerpunkte 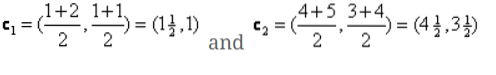
Nachdem wir die neuen Schwerpunkte erhalten haben, sieht das Clustering wie folgt aus:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
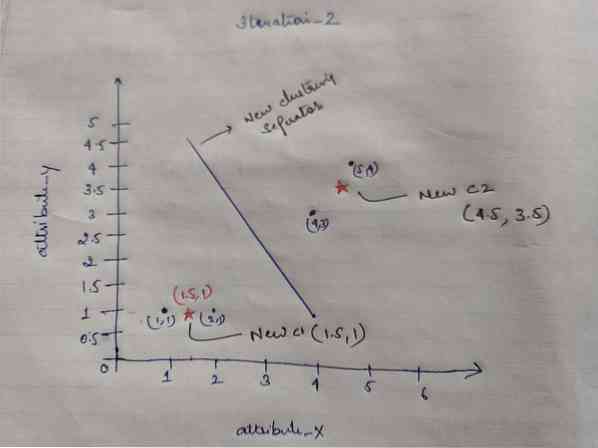
Iteration_2: Wir wiederholen den Schritt, bei dem wir den neuen Abstand jedes Objekts zu den neu berechneten Schwerpunkten berechnen. Nach der Berechnung erhalten wir also die folgende Distanzmatrix für Iteration_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) Cluster1 | Gruppe 1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) Cluster2 | Gruppe_2 |
A B C D
| EIN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Ja |
Auch hier machen wir die Clustering-Zuweisungen basierend auf dem Mindestabstand wie zuvor. Danach haben wir die Clustering-Matrix erhalten, die mit G_1 . identisch ist.
G_2 =
| EIN | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | Gruppe 1 |
| 0 | 0 | 1 | 1 | Gruppe_2 |
Wie hier, G_2 == G_1, Daher ist keine weitere Iteration erforderlich, und wir können hier aufhören.
K-Means-Implementierung mit Python:
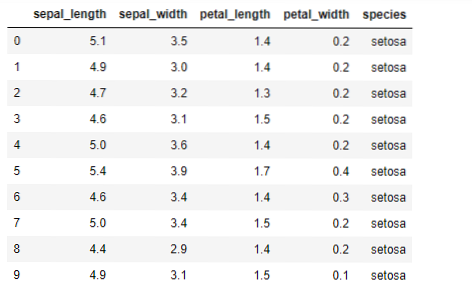
Jetzt implementieren wir den K-Means-Algorithmus in Python. Um die K-Means zu implementieren, werden wir den berühmten Iris-Datensatz verwenden, der Open Source ist. Dieser Datensatz hat drei verschiedene Klassen. Dieser Datensatz hat im Wesentlichen vier Funktionen: Kelchblattlänge, Kelchblattbreite, Kronblattlänge und Kronblattbreite. Die letzte Spalte enthält den Namen der Klasse dieser Zeile wie setosa set.
Der Datensatz sieht wie folgt aus:
Für die Python-K-Means-Implementierung müssen wir die erforderlichen Bibliotheken importieren. Also importieren wir Pandas, Numpy, Matplotlib und auch KMeans von sklearn.Unordnung wie unten angegeben:

Wir lesen die Iris.csv-Datensatz mit der Methode read_csv panda und zeigt die Top-10-Ergebnisse mit der Head-Methode an.
Jetzt lesen wir nur die Features des Datasets, die wir zum Trainieren des Modells benötigt haben. Wir lesen also alle vier Merkmale der Datensätze (Kelchblattlänge, Kelchblattbreite, Blütenblattlänge, Blütenblattbreite). Dazu haben wir die vier Indexwerte [0, 1, 2, 3] an die iloc-Funktion des Datenrahmens (df) des Pandas übergeben, wie unten gezeigt:
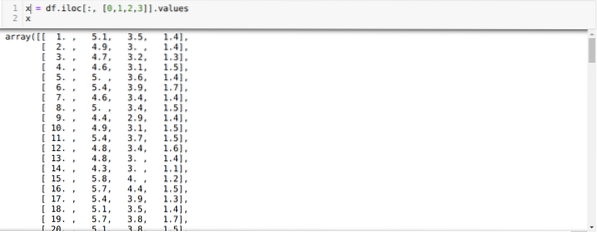
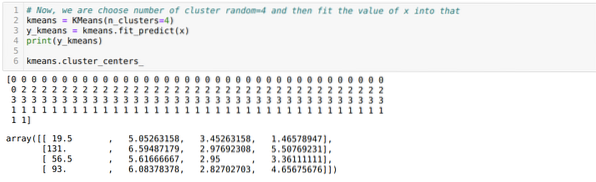
Nun wählen wir die Anzahl der Cluster zufällig (K=5). Wir erstellen das Objekt der K-Means-Klasse und passen dann unseren x-Datensatz zum Training und zur Vorhersage wie unten gezeigt darin an:
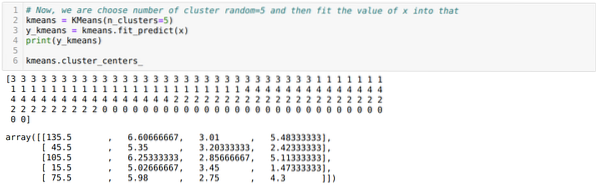
Jetzt visualisieren wir unser Modell mit dem zufälligen K=5-Wert. Wir können deutlich fünf Cluster sehen, aber es sieht so aus, als ob es nicht genau ist, wie unten gezeigt.
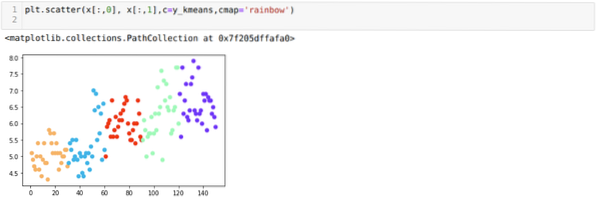
Unser nächster Schritt besteht also darin, herauszufinden, ob die Anzahl der Cluster korrekt war oder nicht. Und dafür verwenden wir die Elbow-Methode. Die Elbow-Methode wird verwendet, um die optimale Anzahl des Clusters für einen bestimmten Datensatz zu ermitteln. Diese Methode wird verwendet, um herauszufinden, ob der Wert von k=5 richtig war oder nicht, da wir keine klare Clusterbildung erhalten. Danach gehen wir zum folgenden Diagramm, das zeigt, dass der Wert von K=5 nicht korrekt ist, da der optimale Wert zwischen 3 oder 4 . liegt.
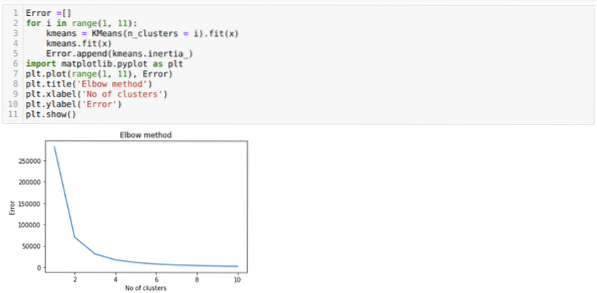
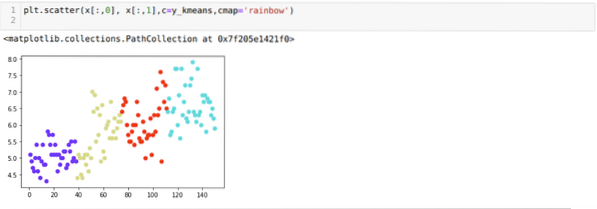
Jetzt führen wir den obigen Code erneut mit der Anzahl der Cluster K = 4 aus, wie unten gezeigt:
Nun visualisieren wir das obige K=4 Neubau-Clustering. Der folgende Bildschirm zeigt, dass das Clustering jetzt über das k-Means erfolgt.
Fazit
Also haben wir den K-Means-Algorithmus sowohl im numerischen als auch im Python-Code untersucht. Wir haben auch gesehen, wie wir die Anzahl der Cluster für einen bestimmten Datensatz herausfinden können. Manchmal kann die Elbow-Methode nicht die richtige Anzahl von Clustern angeben. In diesem Fall gibt es mehrere Methoden, die wir wählen können.
 Phenquestions
Phenquestions


