Wie SciPy ist Open Source, Es hat eine sehr aktive und lebendige Entwickler-Community, aufgrund derer eine enorme Anzahl von Modulen für eine Vielzahl von wissenschaftlichen Anwendungen und Berechnungen mit SciPy verfügbar ist. Einige der komplexen mathematischen Operationen, die mit SciPy ausgeführt werden können, sind:
- Interpolation
- Integration
- Optimierung
- Bildverarbeitung
- Statistiken
- Sonderfunktionsberechnungen etc.
SciPy kann mit den meisten Befehls- und Standardbibliotheken wie der GSL-Bibliothek für C++ und Matlab verglichen werden. Da SciPy auf dem NumPy-Paket aufbaut, können diese beiden Pakete auch vollständig integriert werden. Wenn Ihnen eine mathematische Operation einfällt, die durchgeführt werden muss, überprüfen Sie die SciPy-Bibliothek, bevor Sie dieses Modul selbst implementieren, da SciPy in den meisten Fällen alle Operationen für Sie bereits vollständig implementiert hat.
SciPy-Bibliothek installieren
Lassen Sie uns die SciPy-Bibliothek installieren, bevor wir zu den tatsächlichen Beispielen und Konzepten übergehen. Es gibt zwei Möglichkeiten, dieses Paket zu installieren. Die erste beinhaltet die Verwendung des Python-Paketmanagers pip:
pip installieren scipyDer zweite Weg bezieht sich auf Anaconda, wir können das Paket installieren als:
conda install -c anaconda scipySobald die Bibliothek installiert ist, können wir sie importieren als:
scipy importierenSchließlich werden wir auch NumPy verwenden (es wird empfohlen, dass wir für alle NumPy-Operationen NumPy direkt verwenden, anstatt das SciPy-Paket zu durchlaufen):
numpy importierenEs ist möglich, dass wir in einigen Fällen auch unsere Ergebnisse plotten möchten, für die wir die Matplotlib-Bibliothek verwenden. Führen Sie den folgenden Import für diese Bibliothek aus:
Matplotlib importierenIch werde den Anaconda-Manager für alle Beispiele in dieser Lektion verwenden. Ich werde ein Jupyter Notebook dafür starten:

Nachdem wir nun mit allen Importanweisungen zum Schreiben von Code bereit sind, fangen wir an, mit einigen praktischen Beispielen in das SciPy-Paket einzutauchen.
Arbeiten mit Polynomgleichungen
Wir beginnen mit der Betrachtung einfacher polynomischer Gleichungen. Es gibt zwei Möglichkeiten, wie wir Polynomfunktionen in unser Programm integrieren können. Wir können gebrauchen poly1d Klasse, die Koeffizienten oder die Wurzeln eines Polynoms verwendet, um ein Polynom zu initialisieren. Schauen wir uns ein Beispiel an:
aus numpy import poly1dfirst_polynomial = poly1d([3, 4, 7])
print(erstes_polynom)
Wenn wir dieses Beispiel ausführen, sehen wir die folgende Ausgabe:

Offensichtlich wird die polynomische Darstellung der Gleichung als Ausgabe ausgegeben, sodass das Ergebnis ziemlich leicht zu verstehen ist. Wir können auch verschiedene Operationen an diesem Polynom durchführen, wie zum Beispiel quadrieren, seine Ableitung finden oder sogar nach einem Wert von x . auflösen. Versuchen wir all dies im nächsten Beispiel:
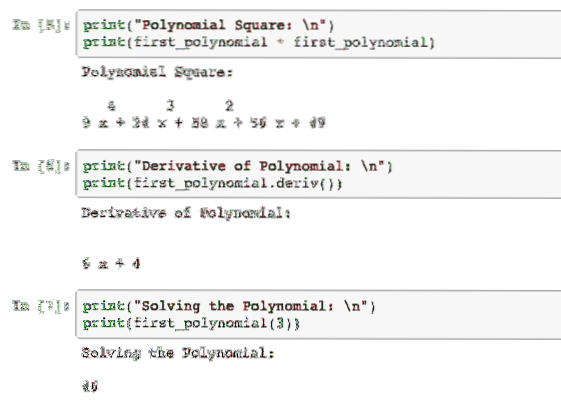
print("Polynomquadrat: \n")print(erstes_polynom * erstes_polynom)
print("Ableitung des Polynoms: \n")
print(first_polynomial.deriv())
print("Das Polynom lösen: \n")
print(erstes_polynom(3))
Wenn wir dieses Beispiel ausführen, sehen wir die folgende Ausgabe:
Gerade als ich dachte, dass das alles ist, was wir mit SciPy machen könnten, fiel mir ein, dass wir auch ein Polynom integrieren können. Lassen Sie uns ein letztes Beispiel mit Polynomen ausführen:
print("Integration des Polynoms: \n")print(first_polynomial.Ganzzahl(1))
Die übergebene ganze Zahl sagt dem Paket, wie oft das Polynom integriert werden soll:
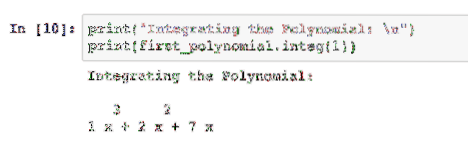
Wir können einfach eine weitere ganze Zahl übergeben, die dem Paket sagt, wie oft dieses Polynom integriert werden soll.
Lineare Gleichungen lösen
Es ist sogar möglich, mit SciPy lineare Gleichungen zu lösen und ihre Wurzeln zu finden, falls sie existieren. Um lineare Gleichungen zu lösen, stellen wir den Gleichungssatz als NumPy-Arrays und ihre Lösung als separate NumPy-Arrays dar. Lassen Sie es uns an einem Beispiel visualisieren, in dem wir dasselbe tun und nutzen linalg Paket, um die Wurzeln der Gleichungen zu finden, hier sind die Gleichungen, die wir lösen werden:
1x + 5y = 63x + 7y = 9
Lösen wir die obigen Gleichungen:
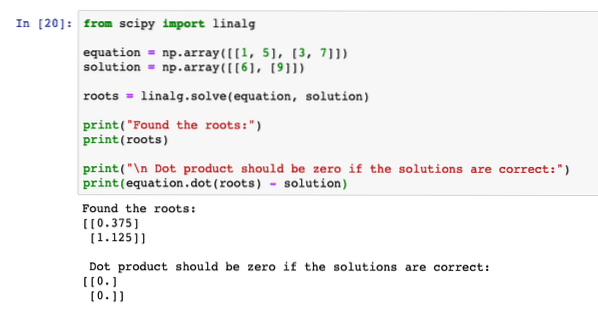
aus scipy import linalgGleichung = np.Array([[1, 5], [3, 7]])
Lösung = np.Array([[6], [9]])
Wurzeln = linalg.lösen (Gleichung, Lösung)
print("Die Wurzeln gefunden:")
Drucken (Wurzeln)
print("\n Das Punktprodukt sollte Null sein, wenn die Lösungen richtig sind:")
drucken (Gleichung.Punkt(Wurzeln) - Lösung)
Wenn wir das obige Programm ausführen, sehen wir, dass die Punktproduktgleichung null Ergebnis liefert, was bedeutet, dass die vom Programm gefundenen Nullstellen korrekt waren:
Fourier-Transformationen mit SciPy
Fourier-Transformationen helfen uns, eine Funktion als separate Komponenten auszudrücken, aus denen diese Funktion besteht, und führt uns über den Weg, wie wir diese Komponenten rekombinieren können, um die ursprüngliche Funktion zurückzubekommen.
Schauen wir uns ein einfaches Beispiel für Fourier-Transformationen an, bei dem wir die Summe zweier Kosinusse mithilfe der Matplotlib-Bibliothek darstellen:
von scipy.fftpack importieren fft# Anzahl der Abtastpunkte
N = 500
# Probenabstand
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N)
y = np.cos(50.0 * 2.0* np.pi * x) + 0.5 * np.cos(80.0 * 2.0 * np.pi * x)
yf = fft(y)
xf = np.linspace(0.0, 1.0/(2.0 * T), N//2)
# matplotlib zum Plotten
Matplotlib importieren.pyplot als plt
plt.Grundstück(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.Titel('Info')
plt.ylabel('Y-Achse')
plt.xlabel('X-Achse')
plt.Gitter()
plt.Show()
Hier haben wir mit der Konstruktion eines Abtastraums und einer Kosinusgleichung begonnen, die wir dann transformiert und aufgetragen haben. Hier die Ausgabe des obigen Programms:
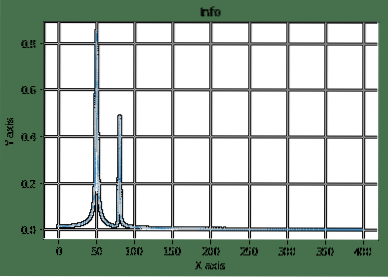
Dies ist eines der guten Beispiele, in denen SciPy in einer komplexen mathematischen Gleichung verwendet wird, um Dinge leicht zu visualisieren.
Vektoren und Matrix mit SciPy
Da wir jetzt viele Dinge wissen, zu denen SciPy fähig ist, können wir sicher sein, dass SciPy auch mit Vektoren und Matrix arbeiten kann. Die Matrizen sind ein wichtiger Teil der linearen Algebra, da wir auch Matrizen verwenden, um Vektorabbildungen darzustellen.
So wie wir mit SciPy lineare Gleichungen lösen wollten, können wir Vektoren mit darstellen np.Array() Funktionen. Beginnen wir mit der Konstruktion einer Matrix:
meine_matrix = np.Matrix(np.zufällig.zufällig((3, 3)))print(meine_matrix)
Hier ist die Ausgabe des obigen Snippets:

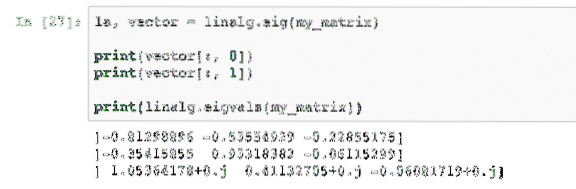
Immer wenn wir von Matrizen sprechen, sprechen wir immer von Eigenwerten und Eigenvektoren. Einfach ausgedrückt sind Eigenvektoren die Vektoren, die bei Multiplikation mit einer Matrix ihre Richtung nicht ändern, im Gegensatz zu den meisten Vektoren. Dies bedeutet, dass selbst wenn Sie einen Eigenvektor mit einer Matrix multiplizieren, es einen Wert (oder Eigenwert) gibt, der einer der Faktoren der Multiplikation ist. Das heisst:
Ax = λx.In der obigen Gleichung ist A die Matrix, λ ist der Eigenwert und x ist der Vektor. Lassen Sie uns ein einfaches Code-Snippet schreiben, um die Eigenwerte für einen bestimmten Vektor zu finden:
la, Vektor = linalg.eig(meine_matrix)drucken(vektor[:, 0])
drucken(vektor[:, 1])
drucken (linalg.eigvals(meine_matrix))
Wenn wir dieses Beispiel ausführen, sehen wir die folgende Ausgabe:
Berechnung der Matrixdeterminante
Die nächste Operation, die wir mit SciPy ausführen werden, ist die Berechnung der Determinante einer 2-dimensionalen Matrix. Wir werden die Matrix, die wir im letzten Code-Snippet verwendet haben, hier wiederverwenden:
linalg.det(meine_matrix)Wenn wir dieses Beispiel ausführen, sehen wir die folgende Ausgabe:

Fazit
In dieser Lektion haben wir uns viele gute Beispiele angesehen, bei denen SciPy uns helfen kann, indem es komplexe mathematische Berechnungen für uns mit einer einfach zu verwendenden API und Paketen durchführt.
 Phenquestions
Phenquestions